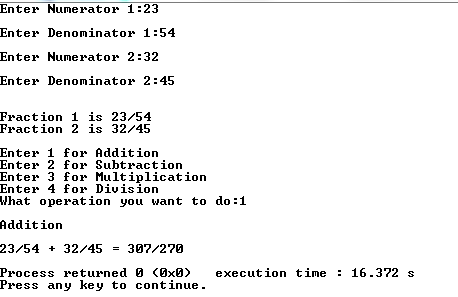
C++ | Using Simpsons Rule to Numerically integrate an equation !
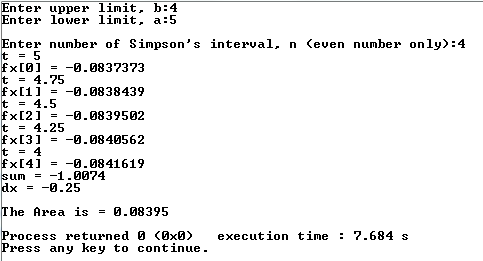
So here is the code and the explanation below : #include <iostream> #include <cmath> using namespace std; main(){ int a,b,n; cout << "Enter upper limit, b:"; cin >> b; cout << "Enter lower limit, a:"; cin >> a; cout << "\nEnter number of Simpson's interval, n (even number only):"; cin >> n; long double dx, t=0; dx = (long double)(b-a)/n; long double fx[n+1]; for(int i=0;i<=n;i++){ if (i == 0){ t = a; } else if (i == n){ t = b; } else{ t = a+(i*dx); } //cout << "t = " << t << endl; // im just curious to know fx[i] = (1.36*pow(10,-10))*t*t*t*t - (1.23*pow(10,-7))*t*t*t + (4.12*pow(10,-6))*t*t + (3.95*pow(10,-4))*t - (8.58*pow(10,-2)); //fx[i] = (double)1 / (t + 1 ); //cout << "fx[" << i << "] = ...